מדידת השראות סינכרונית של מנועי מגנט קבוע

א. המטרה והמשמעות של מדידת השראות סינכרונית
(1) מטרת מדידת הפרמטרים של השראות סינכרונית (כלומר השראות ציר-רוחב)
פרמטרי ההשראות AC ו-DC הם שני הפרמטרים החשובים ביותר במנוע סינכרוני בעל מגנט קבוע. רכישתם המדויקת היא תנאי הכרחי ובסיס לחישוב מאפייני המנוע, סימולציה דינמית ובקרת מהירות. ניתן להשתמש בהשראות הסינכרונית לחישוב מאפייני מצב יציב רבים כגון גורם הספק, יעילות, מומנט, זרם ארמטורה, הספק ופרמטרים אחרים. במערכת הבקרה של מנוע מגנט קבוע המשתמשת בבקרת וקטור, פרמטרי המשרן הסינכרוני מעורבים ישירות באלגוריתם הבקרה, ותוצאות המחקר מראות שבאזור המגנטי החלש, חוסר הדיוק של פרמטרי המנוע יכול להוביל לירידה משמעותית במומנט ובהספק. זה מראה את חשיבותם של פרמטרי המשרן הסינכרוני.
(2) בעיות שיש לשים לב אליהן במדידת השראות סינכרונית
על מנת להשיג צפיפות הספק גבוהה, מבנה מנועים סינכרוניים בעלי מגנט קבוע מתוכנן לעתים קרובות להיות מורכב יותר, והמעגל המגנטי של המנוע רווי יותר, מה שמביא לכך שפרמטר ההשראות הסינכרוניות של המנוע משתנה עם הרוויה של המעגל המגנטי. במילים אחרות, הפרמטרים ישתנו עם תנאי הפעולה של המנוע, כאשר תנאי הפעולה המדורגים לחלוטין של פרמטרי ההשראות הסינכרוניות אינם יכולים לשקף במדויק את אופי פרמטרי המנוע. לכן, יש צורך למדוד את ערכי ההשראות בתנאי הפעלה שונים.
2. שיטות מדידה של השראות סינכרוניות של מנוע מגנט קבוע
מאמר זה אוסף שיטות שונות למדידת השראות סינכרוניות ועורך השוואה וניתוח מפורטות שלהן. ניתן לסווג שיטות אלו באופן גס לשני סוגים עיקריים: בדיקת עומס ישירה ובדיקה סטטית עקיפה. בדיקה סטטית מחולקת עוד לבדיקה סטטית AC ובדיקה סטטית DC. כיום, הפרק הראשון של "שיטות בדיקת השראות סינכרוניות" שלנו יסביר את שיטת בדיקת העומס.

ספרות [1] מציגה את עקרון שיטת העומס הישיר. בדרך כלל ניתן לנתח מנועים בעלי מגנט קבוע באמצעות תורת התגובה הכפולה כדי לנתח את פעולת העומס שלהם, ודיאגרמות הפאזה של פעולת הגנרטור והמנוע מוצגות באיור 1 להלן. זווית ההספק θ של הגנרטור חיובית כאשר E0 עולה על U, זווית מקדם ההספק φ חיובית כאשר I עולה על U, וזווית מקדם ההספק הפנימית ψ חיובית כאשר E0 עולה על I. זווית ההספק θ של המנוע חיובית כאשר U עולה על E0, זווית מקדם ההספק φ חיובית כאשר U עולה על I, וזווית מקדם ההספק הפנימית ψ חיובית כאשר I עולה על E0.

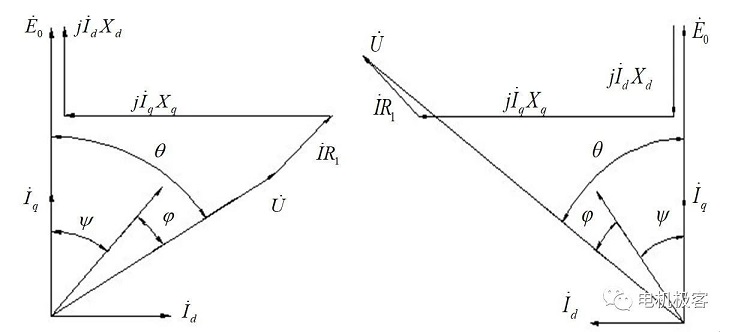
איור 1 דיאגרמת פאזות של פעולת מנוע סינכרוני בעל מגנט קבוע
(א) מצב גנרטור (ב) מצב מנוע

על פי דיאגרמת פאזות זו ניתן לקבל: כאשר מנוע המגנט הקבוע פועל בעומס, נמדד כוח האלקטרו-מניע E0 של העירור ללא עומס, מתח מסוף הארמטורה U, זרם I, זווית גורם ההספק φ וזווית ההספק θ וכן הלאה. ניתן לקבל את זרם הארמטורה של הציר הישר, כאשר רכיב הציר הרוחב Id = Isin (θ - φ) ו-Iq = Icos (θ - φ), אז ניתן לקבל את Xd ו-Xq מהמשוואה הבאה:

כאשר הגנרטור פועל:

Xd=[E0-Ucosθ-IR1cos(θ-φ)]/Id (1)
Xq=[Usinθ+IR1sin(θ-φ)]/Iq (2)

כאשר המנוע פועל:

Xd=[E0-Ucosθ+IR1cos(θ-φ)]/Id (3)
Xq=[Usinθ-IR1sin(θ-φ)]/Iq (4)

פרמטרי המצב היציב של מנועים סינכרוניים בעלי מגנט קבוע משתנים ככל שתנאי הפעולה של המנוע משתנים, וכאשר זרם הארמטורה משתנה, גם Xd וגם Xq משתנים. לכן, בעת קביעת הפרמטרים, יש לוודא ציון גם של תנאי הפעולה של המנוע. (כמות זרם הציר החילופין והישר או זרם הסטטור וזווית מקדם ההספק הפנימית)

הקושי העיקרי במדידת הפרמטרים האינדוקטיביים בשיטת העומס הישיר טמון במדידת זווית ההספק θ. כידוע, זהו הפרש זווית הפאזה בין מתח הדק המנוע U לבין הכוח האלקטרו-מוטיב העירור. כאשר המנוע פועל ביציבות, ניתן לקבל את מתח הקצה ישירות, אך לא ניתן לקבל את E0 ישירות, ולכן ניתן לקבל אותו רק בשיטה עקיפה כדי לקבל אות מחזורי בעל תדר זהה ל-E0 והפרש פאזה קבוע שיחליף את E0 על מנת לבצע השוואת פאזה עם מתח הקצה.

השיטות העקיפות המסורתיות הן:
1) בחריץ הארמטורה של המנוע הנבדק, קבור את הזווית של מספר סיבובים של חוט דק כסליל מדידה, על מנת לקבל את אותה אות השוואת מתח עם סליל המנוע הנבדק, באמצעות השוואת זווית מקדם ההספק ניתן להשיג.
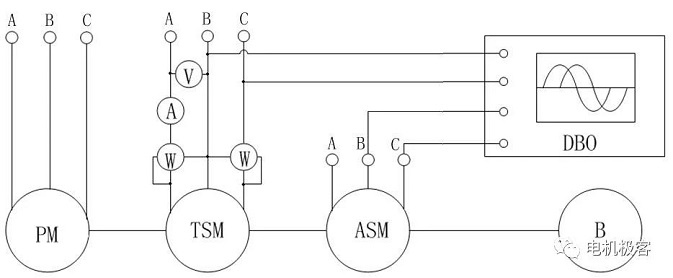
2) התקן מנוע סינכרוני על ציר המנוע הנבדק, הזהה למנוע הנבדק. שיטת מדידת פאזת המתח [2], שתתואר להלן, מבוססת על עיקרון זה. דיאגרמת החיבור הניסיונית מוצגת באיור 2. ה-TSM הוא מנוע סינכרוני בעל מגנט קבוע הנבדק, ה-ASM הוא מנוע סינכרוני זהה הנדרש בנוסף, ה-PM הוא המנוע הראשי, שיכול להיות מנוע סינכרוני או מנוע DC, B הוא הבלם, וה-DBO הוא אוסצילוסקופ בעל קרן כפולה. הפאזות B ו-C של ה-TSM וה-ASM מחוברות לאוסצילוסקופ. כאשר ה-TSM מחובר לספק כוח תלת פאזי, האוסילוסקופ מקבל את האותות VTSM ו-E0ASM. מכיוון ששני המנועים זהים ומסובבים באופן סינכרוני, פוטנציאל הנגד ללא עומס של ה-TSM של הבוחן ופוטנציאל הנגד ללא עומס של ה-ASM, הפועל כגנרטור, E0ASM, נמצאים בפאזה. לכן, ניתן למדוד את זווית ההספק θ, כלומר, הפרש הפאזה בין VTSM ל-E0ASM.

איור 2 דיאגרמת חיווט ניסיונית למדידת זווית הספק

שיטה זו אינה נפוצה במיוחד, בעיקר משום ש: ① מנוע סינכרוני קטן או שנאי סיבובי המותקן בציר הרוטור, לצורך מדידה יש ​​למנוע בעל שני צירים מורחבים, דבר שלעתים קרובות קשה לעשות. ② דיוק מדידת זווית ההספק תלוי במידה רבה בתוכן ההרמוני הגבוה של VTSM ו-E0ASM, ואם תוכן ההרמוני גדול יחסית, דיוק המדידה יופחת.
3) כדי לשפר את דיוק בדיקת זווית ההספק וקלות השימוש, כעת נעשה שימוש רב יותר בחיישני מיקום לזיהוי אות מיקום הרוטור, ולאחר מכן השוואת פאזות עם גישת מתח הקצה.
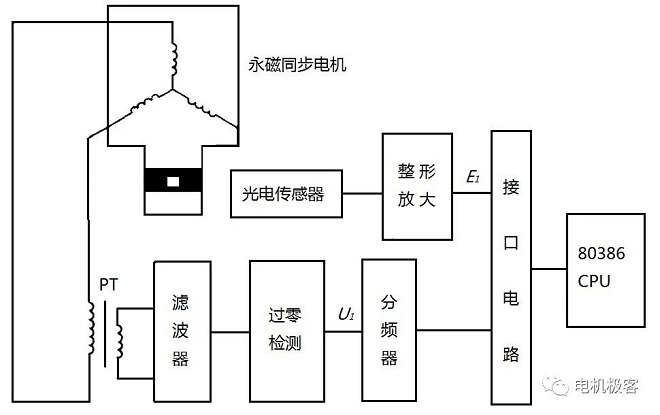
העיקרון הבסיסי הוא להתקין דיסק פוטואלקטרי מוקרן או מוחזר על ציר המנוע הסינכרוני בעל המגנט הקבוע הנמדד, מספר החורים המפוזרים באופן אחיד על הדיסק או סמנים שחורים ולבנים ומספר זוגות הקטבים של המנוע הסינכרוני הנבדק. כאשר הדיסק מסתובב סיבוב אחד עם המנוע, החיישן הפוטואלקטרי מקבל אותות מיקום רוטור p ומייצר p פולסים במתח נמוך. כאשר המנוע פועל באופן סינכרוני, תדירות אות מיקום הרוטור שווה לתדירות מתח הדק הארמטורה, והמופע שלו משקף את המופע של הכוח האלקטרו-מונע העירור. אות פולס הסינכרון מוגבר על ידי עיצוב, הזזת פאזה ומתח הארמטורה של המנוע הנבדק לצורך השוואת פאזה כדי לקבל את הפרש הפאזה. כאשר המנוע פועל ללא עומס, הפרש הפאזה הוא θ1 (בקירוב, זווית ההספק θ = 0 בזמן זה), כאשר העומס פועל, הפרש הפאזה הוא θ2, אז הפרש הפאזה θ2 - θ1 הוא ערך זווית ההספק הנמדד של עומס המנוע הסינכרוני בעל המגנט הקבוע. הדיאגרמה הסכמטית מוצגת באיור 3.

איור 3 תרשים סכמטי של מדידת זווית הספק

מכיוון שקשה יותר לבדוק דיסק פוטואלקטרי עם סימן שחור ולבן, קשה יותר לסמן אותו באופן אחיד בדיסק פוטואלקטרי, וכאשר קוטבי המנוע הסינכרוני של המגנט הקבוע נמדדים בו זמנית, הדיסק לא יכול להיות משותף זה לזה. לשם הפשטות, ניתן גם לבדוק את ציר ההינע של המנוע המגנט הקבוע, עטוף בעיגול של סרט שחור, מצופה בסימן לבן, כאשר מקור האור הנפלט מהסרט נאסף בעיגול זה על פני השטח של הסרט. בדרך זו, בכל סיבוב של המנוע, החיישן הפוטואלקטרי בטרנזיסטור הרגיש לאור מקבל אור מוחזר והולכה פעם אחת, וכתוצאה מכך נוצר אות פולס חשמלי, לאחר הגברה ועיצוב לקבלת אות השוואה E1. מקצה סליל ארמטורה של המנוע הנבדק, מתח דו-פאזי כלשהו יורד על ידי שנאי המתח PT למתח נמוך, הנשלח למשוואת המתח, ויוצר אות פולס מתח מלבני מייצג של הפאזה U1. U1 באמצעות תדר p, ומשווה הפאזה כדי לקבל השוואה בין הפאזה למשוואת הפאזה. U1 באמצעות תדר p, ומשווה הפאזה כדי להשוות את הפרש הפאזה שלו לאות.
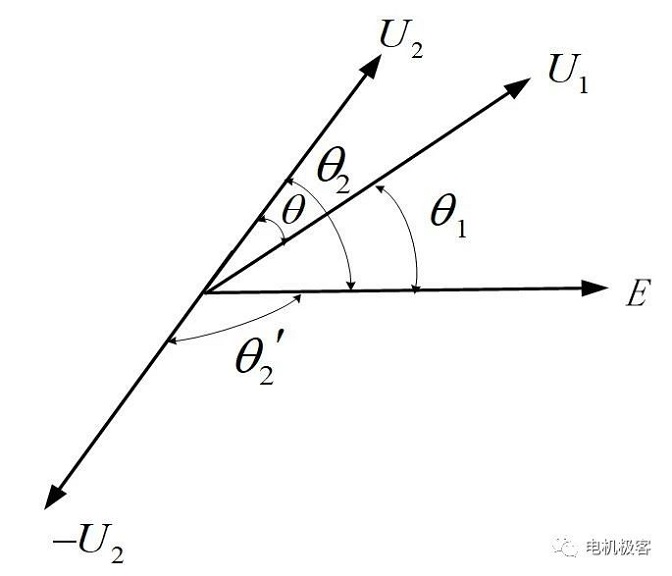
החיסרון של שיטת מדידת זווית ההספק הנ"ל הוא שיש לבצע את ההפרש בין שתי המדידות כדי לקבל את זווית ההספק. על מנת להימנע מחיסור של שני כמויות ולהפחית את הדיוק, במדידת הפרש הפאזה של העומס θ2, היפוך אות U2, הפרש הפאזה הנמדד הוא θ2'=180° - θ2, זווית ההספק θ=180° - (θ1 + θ2'), מה שממיר את שני הכמויות מחיסור הפאזה לחיבור. דיאגרמת כמויות הפאזה מוצגת באיור 4.

איור 4 עקרון שיטת חיבור הפאזה לחישוב הפרש הפאזה

שיטה משופרת נוספת אינה משתמשת בחלוקת תדר של אות צורת גל מלבנית של מתח, אלא משתמשת במיקרו-מחשב כדי להקליט בו זמנית את צורת הגל של האות, בהתאמה, דרך ממשק הקלט, להקליט את צורות הגל של מתח ללא עומס ואות מיקום הרוטור U0, E0, כמו גם את אותות צורת הגל המלבניים של מתח העומס ומיקום הרוטור U1, E1, ולאחר מכן להזיז את צורות הגל של שתי ההקלטות זו ביחס לזו עד שצורות הגל של שני אותות צורת הגל המלבניים של מתח חופפות לחלוטין, כאשר הפרש הפאזה בין שני אותות מיקום הרוטור הוא זווית ההספק; או להזיז את צורת הגל כך ששתי צורות הגל של אותות מיקום הרוטור חופפות, אז הפרש הפאזה בין שני אותות המתח הוא זווית ההספק.
יש לציין כי בפעולה בפועל ללא עומס של מנוע סינכרוני עם מגנט קבוע, זווית ההספק אינה אפס, במיוחד עבור מנועים קטנים. עקב אובדן גדול יחסית בפעולה ללא עומס (כולל אובדן נחושת בסטטור, אובדן ברזל, אובדן מכני, אובדן תועה) זווית ההספק אפס תגרום לשגיאה גדולה במדידת זווית ההספק. ניתן להשתמש בה כדי לגרום למנוע DC לפעול במצב המנוע, כיוון ההיגוי והיגוי מנוע הבדיקה להיות עקביים. עם היגוי מנוע DC, מנוע DC יכול לפעול באותו מצב, וניתן להשתמש במנוע DC כמנוע בדיקה. זה יכול לגרום למנוע DC לפעול במצב המנוע, כיוון ההיגוי והיגוי מנוע הבדיקה להיות עקביים, כך שמנוע DC יספק את כל אובדן הציר של מנוע הבדיקה (כולל אובדן ברזל, אובדן מכני, אובדן תועה וכו'). שיטת השיפוט היא שהספק הקלט של מנוע הבדיקה שווה לצריכת הנחושת של הסטטור, כלומר, P1 = pCu, והמתח והזרם נמצאים בפאזה. הפעם, ה-θ1 הנמדד מתאים לזווית ההספק אפס.
סיכום: יתרונות השיטה:
① שיטת העומס הישיר יכולה למדוד את השראות הרוויה במצב יציב תחת מצבי עומס שונים, ואינה דורשת אסטרטגיית בקרה, שהיא אינטואיטיבית ופשוטה.
מכיוון שהמדידה מתבצעת ישירות תחת עומס, ניתן לקחת בחשבון את אפקט הרוויה ואת השפעת זרם הדה-מגנטיזציה על פרמטרי ההשראות.
חסרונות של שיטה זו:
① שיטת העומס הישיר דורשת מדידה של כמויות גדולות יותר בו זמנית (מתח תלת פאזי, זרם תלת פאזי, זווית מקדם הספק וכו'), מדידת זווית ההספק קשה יותר, ודיוק הבדיקה של כל גודל משפיע ישירות על דיוק חישובי הפרמטרים, וכל מיני שגיאות בבדיקת הפרמטרים קלות להצטבר. לכן, בעת שימוש בשיטת העומס הישיר למדידת פרמטרים, יש לשים לב לניתוח השגיאות, ולבחור דיוק גבוה יותר של מכשיר הבדיקה.
② ערך הכוח האלקטרו-מוטיבי העירור E0 בשיטת מדידה זו מוחלף ישירות על ידי מתח מסוף המנוע ללא עומס, וקירוב זה מביא גם הוא לשגיאות אינהרנטיות. מכיוון שנקודת הפעולה של המגנט הקבוע משתנה עם העומס, מה שאומר שבזרמי סטטור שונים, החדירות וצפיפות השטף של המגנט הקבוע שונים, כך שגם הכוח האלקטרו-מוטיבי העירור המתקבל שונה. בדרך זו, החלפת הכוח האלקטרו-מוטיבי העירור בתנאי עומס בכוח האלקטרו-מוטיבי העירור ללא עומס אינה מדויקת במיוחד.
הפניות
[1] טאנג רניואן ואחרים. תיאוריה ותכנון של מנועי מגנט קבוע מודרניים. בייג'ינג: הוצאת תעשיית המכונות. מרץ 2011
[2] ג'יי. אף. גירס, מ. ווינג. טכנולוגיית מנועים בעלי מגנט קבוע, תכנון ויישומים, מהדורה שנייה. ניו יורק: מרסל דקר, 2002: 170~171
זכויות יוצרים: מאמר זה הוא הדפסה מחודשת של הצצה של מנוע המספר הציבורי של WeChat (电机极客), הקישור המקוריhttps://mp.weixin.qq.com/s/Swb2QnApcCWgbLlt9jMp0A

מאמר זה אינו מייצג את עמדות החברה שלנו. אם יש לכם דעות או השקפות שונות, אנא תקנו אותנו!